8 The pn Junction Diode
8.1 The pn Junction Current
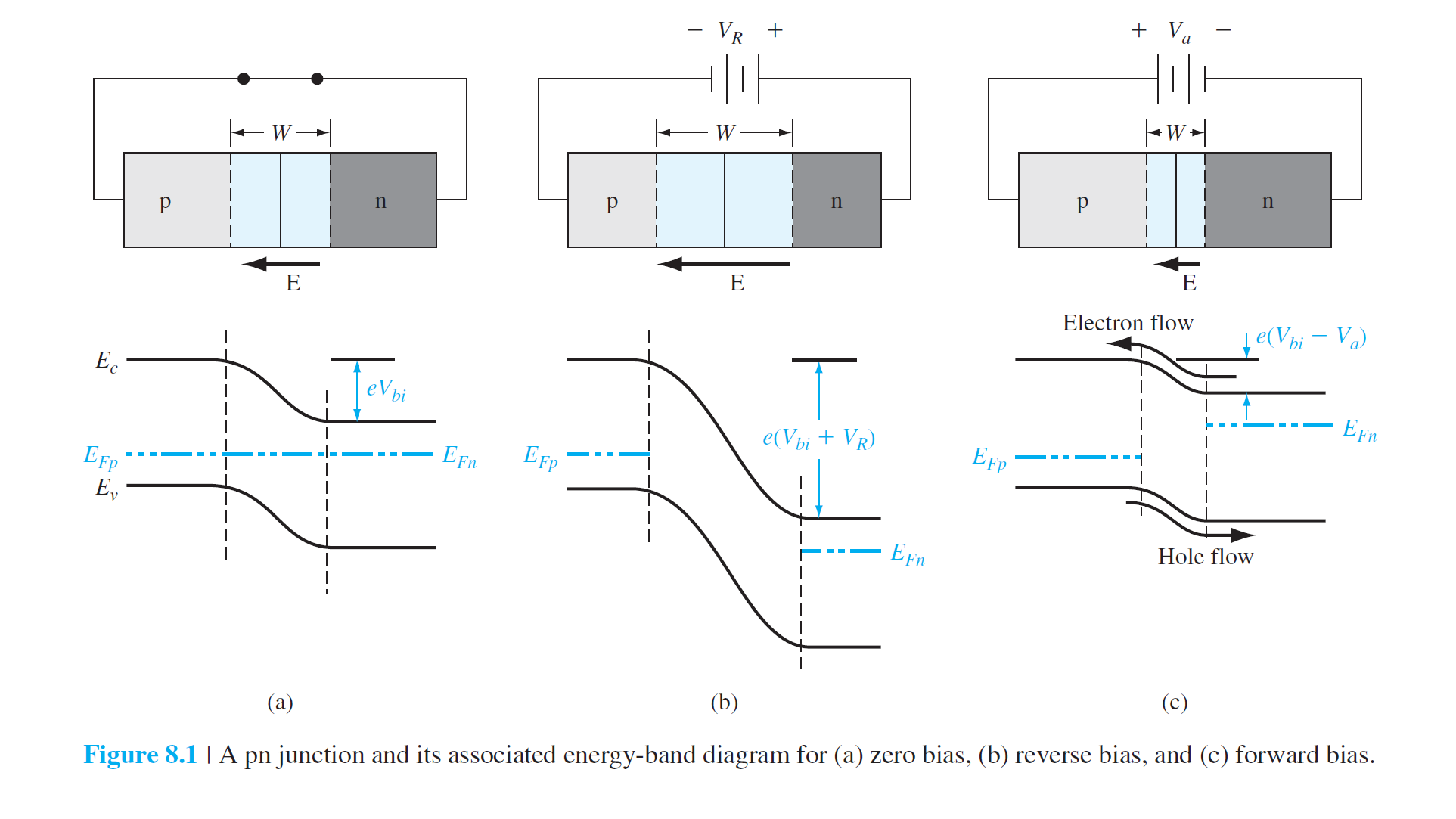
注入到n区的空穴,为n区中的少数载流子
注入到p区的电子,为p区的少数载流子
8.1.2 Ideal Current–Voltage Relationship
- The abrupt depletion layer approximation applies. The space charge regions have abrupt boundaries, and the semiconductor is neutral outside of the depletion region.
- The Maxwell–Boltzmann approximation applies to carrier statistics.
- The concepts of low injection and complete ionization apply.
- The total current is a constant throughout the entire pn structure.
- The individual electron and hole currents are continuous functions through the pn structure.
- The individual electron and hole currents are constant throughout the depletion region.

8.1.3 Boundary Conditions
\[
V_{bi}=V_t\ln(\frac{N_aN_d}{n_i^2})
\]
n区中:
\[
n_{n0}\approx N_d
\]
p区中:
\[
n_{p0}\approx\frac{n_i^2}{N_a}
\]
\[
n_{p0}=n_{n0}\exp(\frac{-eV_{bi}}{kT})
\]
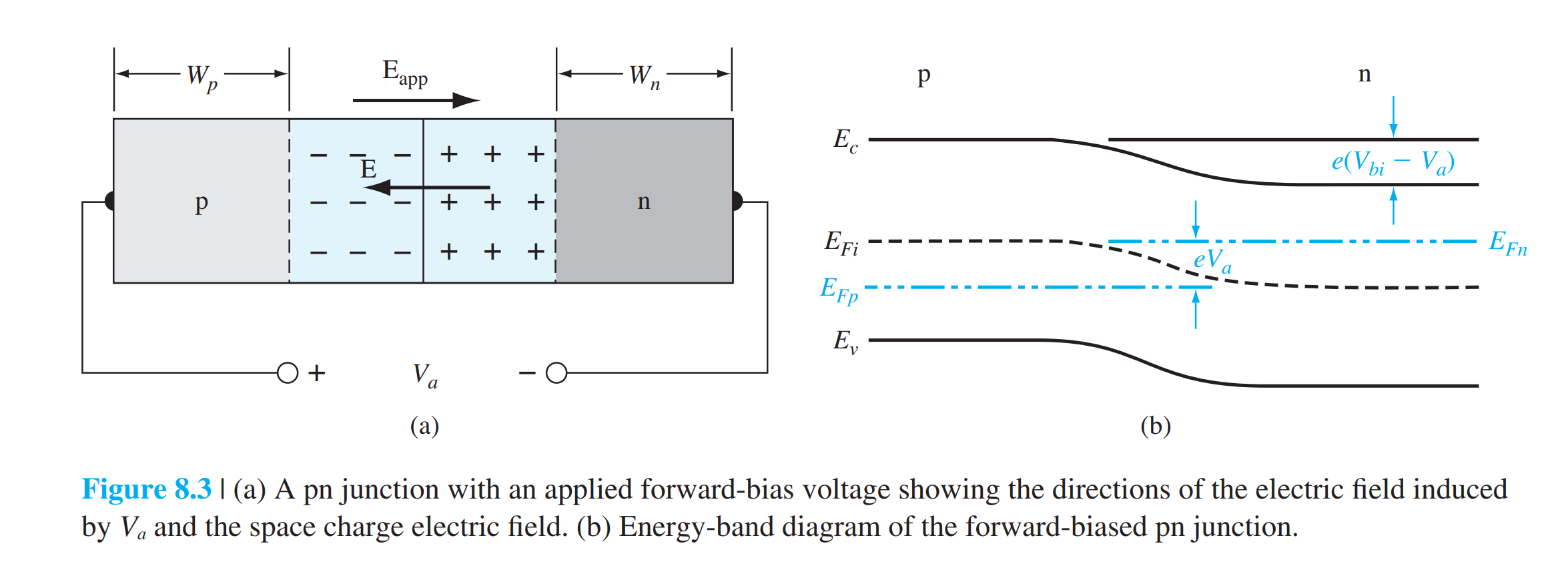
\[
n_p=n_{n0}\exp(\frac{-e(V_{bi}-V_a)}{kT})=n_{n0}\exp(\frac{-eV_{bi}}{kT})\exp(\frac{eV_a}{kT})
\]
\[
n_p=n_{p0}\exp(\frac{eV_a}{kT})
\]
同理:
$$
p_n=p_{n0}\exp(\frac{eV_a}{kT})
$$
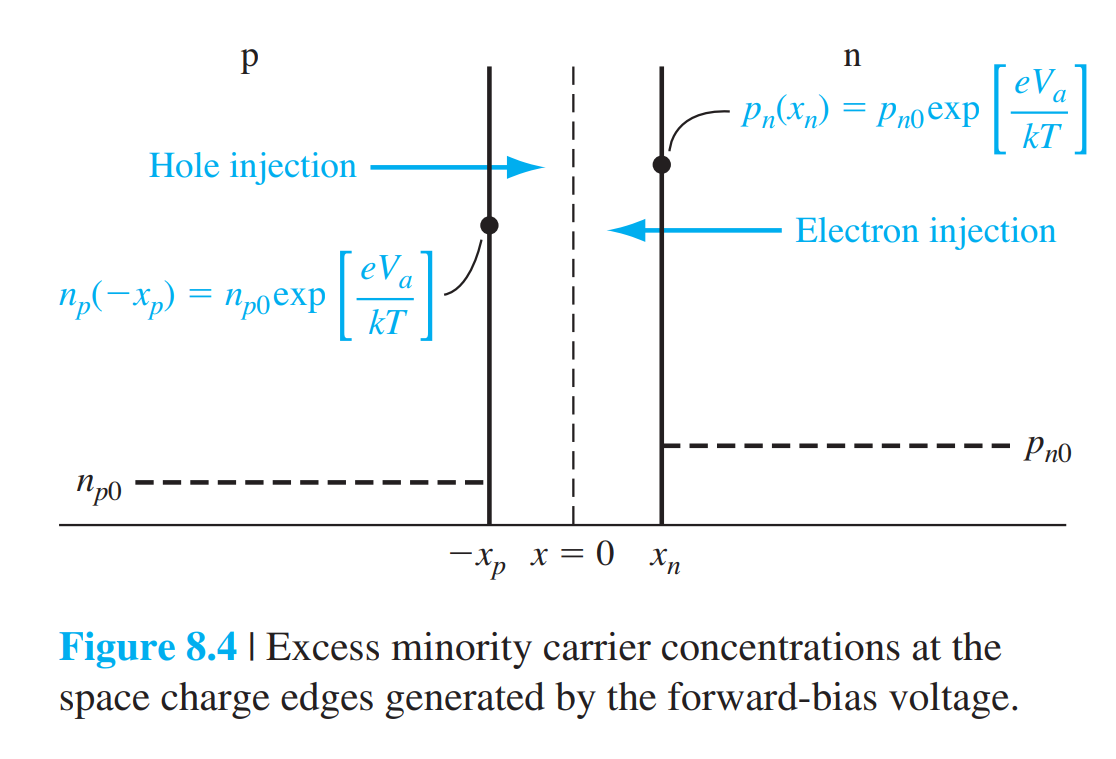
8.1.4 Minority Carrier Distribution
\[
D_p\frac{\partial^2(\delta p_n)}{\partial x^2}-\mu_pE\frac{\partial (\delta p_n)}{\partial x}+g'-\frac{\delta p_n}{\tau_{p0}}=\frac{\partial(\delta p_n)}{\partial t}
\]
- 一级近似,电中性区p区与n区电场为0
- \(x>x_n\)区域,\(E=0, g'=0\)
- pn结处于稳态,\(\partial p/\partial t=0\)
\[
\begin{align*}
D_p\frac{\partial^2(\delta p)}{\partial x^2}-\frac{\partial p}{\tau_{p0}}&=0\\
\frac{d^2(\delta p_n)}{d x^2}-\frac{\delta p_n}{L_p^2}&=0\quad (x>x_n)\\
\small{L_p^2=D_p\tau_{p0}}
\end{align*}
\]
\[
\begin{align*}
\frac{d^2(\delta n_p)}{d x^2}-\frac{\delta n_p}{L_n^2}&=0\quad (x<-x_p)\\
\small{L_n^2=D_n\tau_{n0}}
\end{align*}
\]
boundary condition:
\[
\begin{align*}
p_n(x_n)&=p_{n0}\exp(\frac{eV_a}{kT})\\
n_p(-x_p)&=n_{p0}\exp(\frac{eV_a}{kT})\\
p_n(x\rightarrow +\infin)&=p_{n0}\\
p_n(x\rightarrow -\infin)&=n_{p0}\\
\end{align*}
\]
假设,\(W_n>>L_p\),\(W_p>>L_n\)
\[
\delta p_n(x)=p_n(x)-p_{n0}=p_{n0}\left[ \exp(\frac{eV_a}{kT})-1 \right]\exp(\frac{x_n-x}{L_p})
\]
\[
\delta n_p(x)=n_p(x)-n_{p0}=n_{p0}\left[ \exp(\frac{eV_a}{kT})-1 \right]\exp(\frac{x_p+x}{L_n})
\]
8.1.5 Ideal pn Junction Current
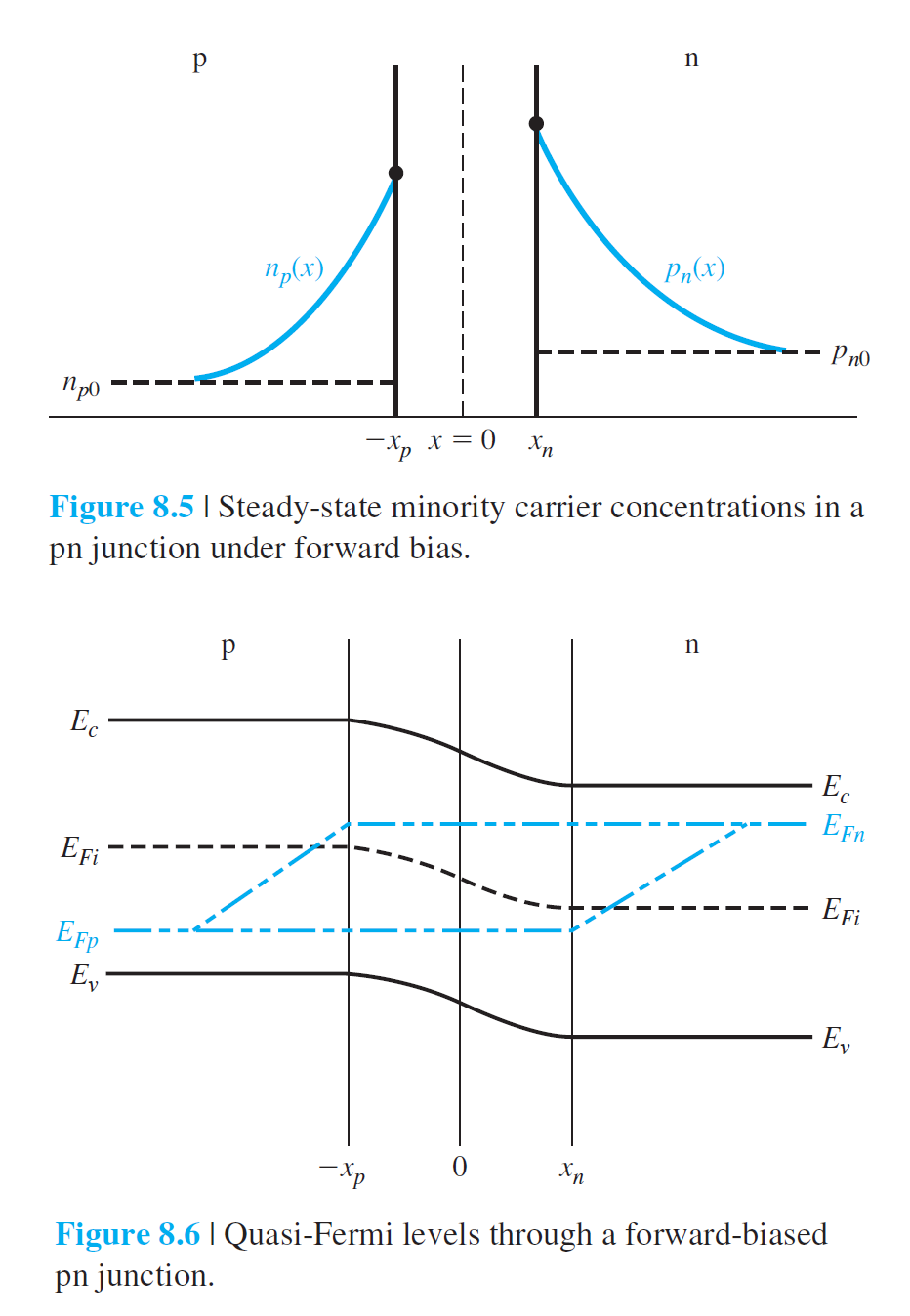
\[
\begin{align*}
J_p(x_n)&=-eD_p\left.\frac{d(\delta p_n(x))}{dx}\right|_{x=x_n}\\
&=\frac{eD_pp_{n0}}{L_p}\left[ \exp(\frac{eV_a}{kT})-1 \right]
\end{align*}
\]
同理:
\[
J_n{(-x_p)}=\frac{eD_nn_{p0}}{L_n}\left[ \exp(\frac{eV_a}{kT})-1 \right]
\]
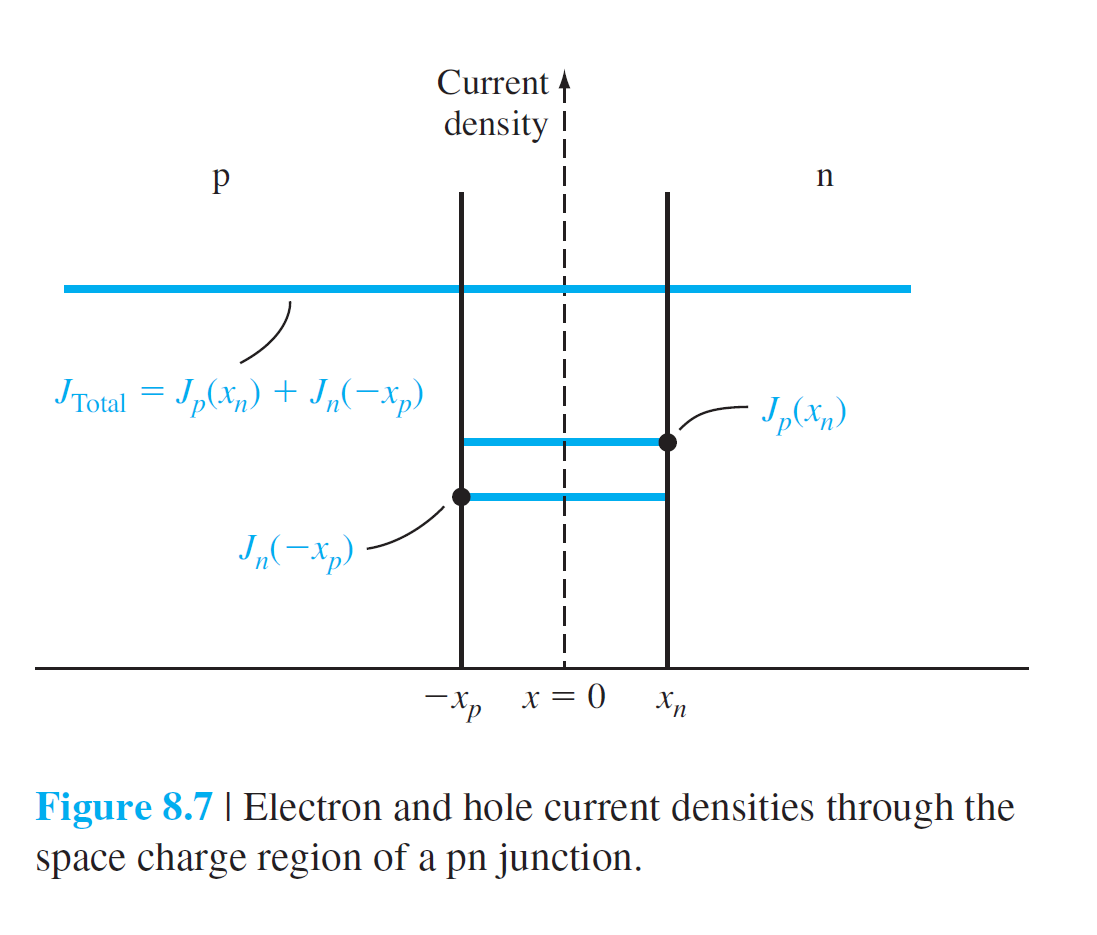
\[
J=J_p(x_n)+J_n(-x_p)=\left[ \frac{eD_pp_{n0}}{L_p}+\frac{eD_nn_{p0}}{L_n} \right]\left[ \exp(\frac{eV_a}{kT})-1 \right]
\]
- \(J_s=\left[ \frac{eD_pp_{n0}}{L_p}+\frac{eD_nn_{p0}}{L_n} \right]\)
\[
J=J_s\left[ \exp(\frac{eV_a}{kT})-1 \right]
\]
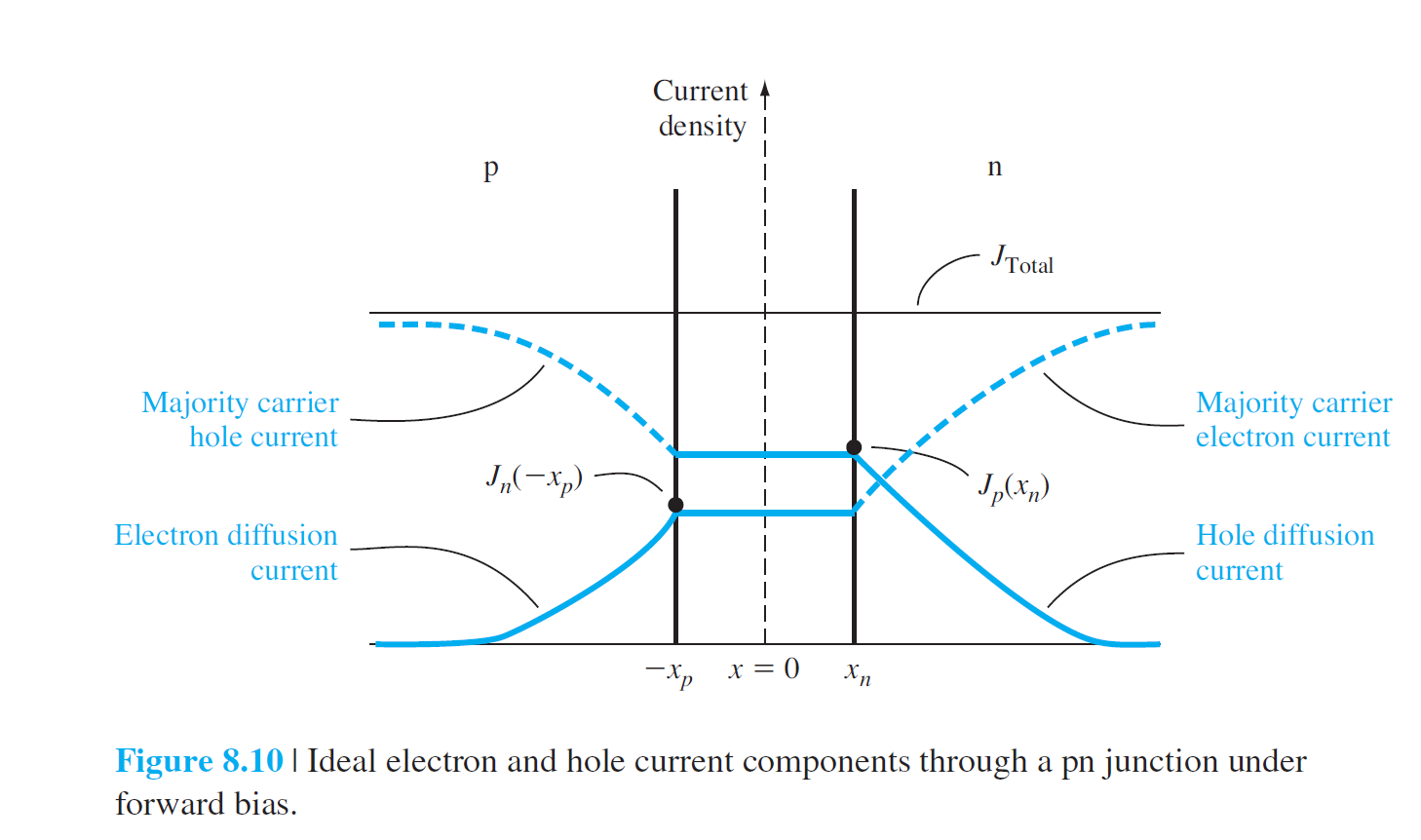
\[
J_p(x)=\frac{eD_pp_{n0}}{L_p}\left[ \exp(\frac{eV_a}{kT})-1 \right]\exp(\frac{x_n-x}{L_p})\quad(x\ge x_n)
\]
\[
J_n{(x)}=\frac{eD_nn_{p0}}{L_n}\left[ \exp(\frac{eV_a}{kT})-1 \right]\exp(\frac{x_p+x}{L_n})\quad(x\le -x_p)
\]
8.1.7 Temperature Effects
对于Si pn结而言,温度每升高10摄氏度,理想反向饱和电流密度大小升高4倍;正向电流不是很明显
8.1.8 The “Short” Diode
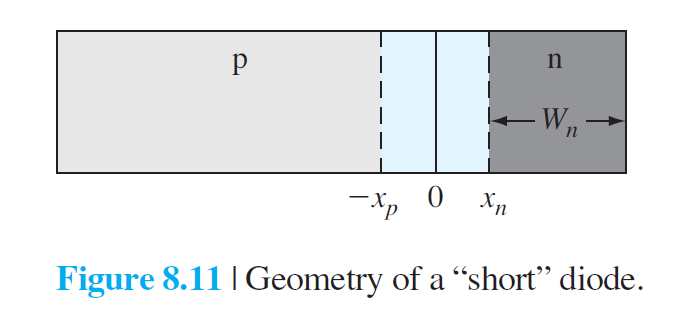
\[
\begin{align*}
\frac{d^2(\delta n_p)}{d x^2}-\frac{\delta n_p}{L_n^2}&=0\quad (x<-x_p)\\
\small{L_n^2=D_n\tau_{n0}}
\end{align*}
\]
\[
\text{boundary condition 1: }p_n(x_n)=p_{n0}\exp(\frac{eV_a}{kT})
\]
假设:
- \(x=(x_n+W_n)\)处有一个欧姆接触,该处的过剩少子浓度为0
\[
\text{boundary condition 2: }p_n(x=x_n+W_n)=p_{n0}
\]
\[
\delta p_n(x)=p_{n0}\left[ \exp(\frac{eV_a}{kT}-1) \right]\frac{\sinh\left[(x_n+W_n-x)/L_p\right]}{\sinh(W_n/L_p)}\approx p_{n0}\left[ \exp(\frac{eV_a}{kT}-1) \right]\left( \frac{x_n+W_n-x}{W_n} \right)
\]
\[
J_p=\frac{eD_pp_{n0}}{W_n}\left[ \exp(\frac{eV_a}{kT}-1) \right]
\]
- \(W_n<<L_p\) 因此扩散电流必读远大于长二极管的扩散电流密度
- n区内勺子的浓度近似为距离的线性函数,因此少子的扩散电流密度为常量,少子内不存在复合过程
8.2 Generation-Recombination Currents and High-Injection Levels
the Shockley– Read–Hall recombination theory
\[
R=\frac{C_nC_pN_t(np-n_i^2)}{C_n(n+n')+C_P(p+p')}
\]
8.2.1 Reverse Biased Generation Current
在空间电荷区,\(n\approx p\approx 0\)
\[
R=\frac{-C_nC_pN_tn_i^2}{C_nn'+C_pp'}
\]
- 为负,电子与空穴一旦产生,就被扫出空间电荷区