WEEK 10

6.5 Network Flow Problems

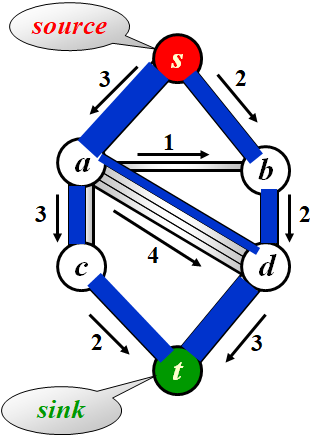
• Determine the maximum amount of flow that can pass from $s$ to $t$.

Note : Total coming in ($v$) = Total going out ($v$) where $v \notin \{ s, t \}$

A Simple Algorithm

• 流图$G_f$表示算法的任意阶段已经达到的流，开始时$G_f$的所有边都没有流，算法终止时$G_f$包含最大流
• 残余图(residual graph)$G_r$表示对于每条边还能添加上多少流，$G_r$的边叫做残余边(residual edge)

Step 1 : Find any path from $s$ to $t$ in $G_r$ , which is called augmenting path(增长通路).

Step 2 : Take the minimum edge on this path as the amount of flow and add to $G_f$.

Step 3 : Update $G_r$ and remove the 0 flow edges.

Step 4 : If there is a path from $s$ to $t$ in $G_r$ then go to Step 1, or end the algorithm.

• Step 1中初始选择的路径可能使算法不能找到最优解，贪心算法行不通

A solution

• allow the algorithm to undo its decisions
• For each edge $( v, w )$ with flow $f_{v, w}$ in $G_f$, add an edge $( w, v )$ with flow $f_{v, w}$ in $G_r$ .

Note : The algorithm works for $G$ with cycles as well.

[Proposition] If the edge capabilities are rational numbers, this algorithm always terminate with a maximum flow.

Analysis

• An augmenting path can be found by an unweighted shortest path algorithm.

• $T=O(f|E|)$ where $f$ is the maximum flow.

• Always choose the augmenting path that allows the largest increase in flow

• 对Dijkstra算法进行单线(single-line)修改来寻找增长通路

• $cap_{max}$为最大边容量
• $O(|E|\log cap_{max})$条增长通路将足以找到最大流，对于增长通路的每次计算需要$O(|E|\log|V|)$时间

$$ T=T_{augmentation}\times T_{find_a_path}\ =O(|E|\log cap_{max})\times O(|E|\log|V|)\ =O(|E|^2\log|V|\log cap_{max}) $$

• Always choose the augmenting path that has the least number of edges

• 使用无权最短路算法来寻找增长路径

$$ T=T_{augmentation}\times T_{find_a_path}\ =O(|E||V|)\times O(|E|)\ =O(|E|^2|V|) $$

Note :

• If every $v \notin \{ s, t \}$ has either a single incoming edge of capacity 1 or a single outgoing edge of capacity 1, then time bound is reduced to $O( |E| |V|^{1/2} )$.
• The min-cost flow problem is to find, among all maximum flows, the one flow of minimum cost provided that each edge has a cost per unit of flow.

---

6.6 Minimum Spanning Tree

[Definition] A spanning tree of a graph $G$ is a tree which consists of $V(G)$ and a subset of $E(G)$

Note :

• The minimum spanning tree is a tree since it is acyclic, the number of edges is $|V|-1$
• It is minimum for the total cost of edges is minimized.
• It is spanning because it covers every vertex.
• A minimum spanning tree exists if $G$ is connected.
• Adding a non-tree edge to a spanning tree, we obtain a cycle.

Greedy Method

Make the best decision for each stage, under the following constrains :

• we must use only edges within the graph
• we must use exactly $|V|-1$ edges
• we may not use edges that would produce a cycle

1. Prim’s Algorithm

2. 在算法的任一时刻，都可以看到一个已经添加到树上的顶点集，而其余顶点尚未加到这棵树中

3. 算法在每一阶段都可以通过选择边$(u, v)$，使得$(u,v)$的值是所有$u$ 在树上但$v$不在树上的边的值中的最小者，而找出一个新的顶点并把它添加到这棵树中

4. Kruskal’s Algorithm

5. 连续地按照最小的权选择边,，并且当所选的边不产生环时就把它作为取定的边

   void Kruskal( Graph G )
   {   
      T = { };
       while ( T contains less than |V|-1 edges && E is not empty ) 
       {
           choose a least cost edge (v, w) from E;  /*DeleteMin*/
           delete (v, w) from E;
           if ( (v, w) does not create a cycle in T )     
              add (v, w) to T;  /*Union/Find*/
           else     
              discard (v, w);
       }
       if ( T contains fewer than |V|-1 edges )
          Error( “No spanning tree” );
   }
   

   void Kruskal(Graph G)
   {
      int EdgesAccepted;
      DisjSet S;
      PriorityQueue H;
      Vertex U, V;
      SetType Uset, Vset;
      Edge E;
   
      Initialize(S);
      ReadGraphIntoHeapArray(G, H);
      BuildHeap(H);
   
      EdgesAccepted = 0;
      while(EdgesAccepted < NumVertex-1)
      {
          E = DeleteMin(H); /*E = (U,V)*/
          Uset = Find(U, S);
          Vset = Find(V, S);
          if(Uset != Vset)
          {
              /*Accept the edge*/
              EdgesAccepted++;
              SetUnion(S, USet, VSet);
          }
      }
   }
   

   $$T=O(|E|\log|E|)$$

   

   ---